Workshop 6 - Jumlah Riemann

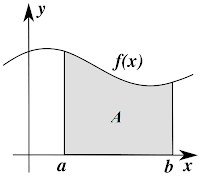
Misalkan f adalah fungsi real pada selang $latex [a,\ b]$, dan misalkan $latex A=\{(x,y)|0<y<f(x)\}$ merupakan daerah di bawah grafik fungsi f dan di antara selang $latex [a,\ b]$. Kita ingin mengukur luas daerah A. Bila kita telah mengukurnya, kita akan melambangkan daerah tersebut sebagai:

$latex \int_{a}^{b}f(x)\ dx$

Gagasan dasar integral Riemann adalah menggunakan hampiran yang sangat sederhana untuk daerah A. Dengan mengambil hampiran yang semakin baik, kita dapat mengatakan "dalam limitnya" kita mendapatkan luas daerah A di bawah kurva.
(Sumber: Wikipedia Indonesia)

Bagaimanakah cara membuat lembar kerja dinamis yang menggambarkan Jumlah Riemann untuk memperkiraan luas daerah antara fungsi dan sumbu x, yang dapat digunakan untuk memperkenalkan konsep integral kepada siswa tersebut?



Langkah Konstruksi

1		Pada kotak input tuliskan rumus fungsi, misalnya f(x)=-0.5x3+2x2–x+1.
2		Buatlah dua titik A and B pada sumbu-x.
		Petunjuk: Kedua titik ini akan menentukan selang (interval) yang membatasi daerah antara fungsi dan sumbu-x.
3		Buatlah slider untuk bilangan n dengan interval 1 sampai dengan 50 and increment 1.
4		Pada kotak input tuliskan “jumlah atas” sebagai berikut: uppersum=UpperSum[f, x(A), x(B), n].
		Petunjuk: x(A) menyatakan absis dari titik A. bilangan n menentukan jumlah persegi panjang yang digunakan dalam menghitung “jumlah bawah”.
5		Pada kotak input tuliskan “jumlah bawah” sebagai berikut: JumlahBawah=LowerSum[f, x(A), x(B), n].
6		Buatlah teks berikut: "Jumlah Atas =" dan klik “JumlahAtas” pada jendela Aljabar.
7		Buatlah teks berikut: "Jumlah Bawah =" dan klik “JumlahBawah” pada jendela Aljabar.
8		Untuk menentukan selisih dari kedua jumlah tersebut, pada kotak input tuliskan: SelisihJumlah=JumlahAtas-JumlahBawah.
9		Buatlah teks berikut: "Selisih =" dan klik “SelisihJumlah” pada jendela Aljabar.
10		Untuk menentukan selisih dari kedua jumlah tersebut, pada kotak input tuliskan: integral=Integral[f, x(A), x(B)].
11		Buatlah teks berikut: "Integral =" dan klik “integral” pada jendela Aljabar.
12		Sekarang aturlah tampilan, tata letak, pewarnaan, dll sesuai dengan yang diinginkan, dengan menggunakan Object Properties.