Dasar penggunaan GeoGebra
o Rangkum sifat (properti) dari bangun (
figure) geometris yang ingin Anda buat.
o Cobalah untuk mencari tahu manakah alat GeoGebra yang dapat digunakan untuk
membuat bangun dengan menggunakan beberapa sifat dari alat tersebut (misalnya,
sudut siku-siku dibuat dengan menggunakan
Perpendicular Line).
o Pastikan, Anda tahu bagaimana menggunakan setiap alat sebelum Anda mulai
konstruksi. Jika Anda tidak tahu cara untuk mengoperasikan alat tertentu, aktifkan
(sorot) alat itu lalu bacalah bantuan
toolbar.
o Untuk masing-masing kegiatan dasar, bukalah
file GeoGebra baru, sembunyikan
jendela aljabar, kotak
input, dan sumbu koordinat.
o Sebaiknya Anda menyimpan
file Anda sebelum Anda memulai aktivitas baru.
o Jangan lupa tombol
Undo dan
Redo jika Anda membuat kesalahan.
o Sering-seringlah menggunakan alat
Move untuk memeriksa konstruksi Anda (misalnya, apakah objek-objek itu benar-
benar telah terhubung, apakah Anda membuat objek-objek yang tidak perlu).
o Jika Anda masih memiliki pertanyaan, bertanyalah kepada rekan yang Anda anggap tahu.
Input Aljabar dan Perintah (Command)
o
Menamai sebuah objek baru, tulislah
nama= di depan pernyataan aljabar. Contoh:
P=(3, 2) berarti membuat titik P.
o
Perkalian harus dimasukkan (
entered) dengan menggunakan tanda bintang (*) atau spasi antara faktor-faktornya.
Contoh: $latex \bf \color{blue}a*x$ atau $latex \bf \color{blue}a\ x$
o
GeoGebra sangat sensitif, dengan demikian huruf besar dan kecil tidak boleh dicampuradukkan.
Catatan:
o
Titik selalu dinamai dengan huruf besar.
Contoh:
A=(1, 2)
o
Ruas garis, garis, lingkaran, fungsi, dll, selalu dinamai dengan huruf kecil.
Contoh: lingkaran $latex \bf c:\ (x-2)^2+(y-1)^2=16$.
o
Variabel $latex x$ dalam fungsi dan variabel $latex x$ dan $latex y$ dalam persamaan irisan kerucut harus selalu huruf kecil.
Contoh: $latex f(x)=3*x+2$
o Jika Anda ingin menggunakan
objek dalam suatu pernyataan aljabar atau perintah, Anda harus membuat objek itu
(melalui kotak
input) sebelum menggunakan namanya.
Contoh:
o $latex \bf \color{blue}y=m*x+b$ membuat garis dengan nilai koefisien $latex m$ dan $latex b$ yang sudah ada (misalnya, berupa nilai
bilangan/
number atau
slider).
o
Line[A,B] membuat garis yang melalui titik A dan B.
o
Tegaskan (konfirmasi) pernyataan yang Anda masukkan pada kotak
input dengan menekan tombol
ENTER.
o
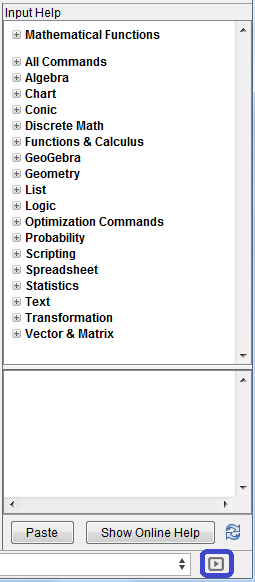
Buka jendela bantuan (help window) dalam penggunaan kotak
input dan perintah (
command) dengan mengklik kotak
Input Help di pojok kanan-bawah.
o
Pesan kesalahan: Selalu membaca pesan - barangkali bisa membantu untuk memperbaiki masalah.
o
Perintah (command) dapat diketikkan atau dipilih dari daftar dalam jendela
Input Help.
Petunjuk: Jika Anda tidak tahu parameter mana yang diminta dalam tanda kurung dari jenis perintah tertentu, ketiklah
perintah itu seutuhnya lalu tekan tombol F1. Sebuah jendela
pop-up akan muncul untuk menjelaskan sintaks dan
parameter yang diperlukan dalam perintah tersebut.
o
Penyelesaian otomatis dari perintah (Automatic completion of commands): Setelah mengetikkan dua huruf pertama
dari perintah ke dalam kotak
input, GeoGebra akan ‘memberitahukan’ perintah itu ‘selengkapnya’.
o Jika GeoGebra menunjukkan perintah yang diinginkan, tekan tombol
ENTER untuk menempatkan kursor di dalam
tanda kurungnya.
o Jika perintah yang disarankan GeoGebra itu bukanlah satu-satunya dari perintah yang ingin Anda masukkan, teruslah
mengetik hingga ditemukan saran yang sesuai.
-->